Matemáticas IV

Las Razones trigonométricas se definen comúnmente como el cociente entre dos lados de un triángulo rectángulo asociado a sus ángulos. Las funciones trigonométricas son funciones cuyos valores son extensiones del concepto de razón trigonométrica en un triángulo rectángulo trazado en unacircunferencia unitaria (de radio unidad). Definiciones más modernas las describen como series infinitas o como la solución de ciertas ecuaciones diferenciales, permitiendo su extensión a valores positivos y negativos, e incluso a números complejos.

Existen seis funciones trigonométricas básicas. Las últimas cuatro, se definen en relación de las dos primeras funciones, aunque se pueden definir geométricamente o por medio de sus relaciones. Algunas funciones fueron comunes antiguamente, y aparecen en las primeras tablas, pero no se utilizan actualmente ; por ejemplo el verseno (1 − cos θ) y la exsecante (sec θ − 1).

Función	Abreviatura	Equivalencias (en radianes)
Seno	sin (sen)	$\sin \; \theta \equiv \frac{1}{\csc \theta} \equiv \cos \left(\frac{\pi}{2} - \theta \right) \equiv \frac{\cos \theta}{\cot \theta} \,$
Coseno	cos	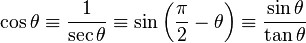$\cos \theta \equiv \frac{1}{\sec \theta} \equiv \sin \left(\frac{\pi}{2} - \theta \right) \equiv \frac{\sin \theta}{\tan \theta} \,$
Tangente	tan	$\tan \theta \equiv \frac{1}{\cot \theta} \equiv \cot \left(\frac{\pi}{2} - \theta \right) \equiv \frac{\sin \theta}{\cos \theta} \,$
Cotangente	ctg (cot)	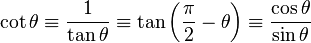$\cot \theta \equiv \frac{1}{\tan \theta} \equiv \tan \left(\frac{\pi}{2} - \theta \right) \equiv \frac{\cos \theta}{\sin \theta} \,$
Secante	sec	$\sec \theta \equiv \frac{1}{\cos \theta} \equiv \csc \left(\frac{\pi}{2} - \theta \right) \equiv \frac{\tan \theta}{\sin \theta} \,$
Cosecante	csc (cosec)	$\csc \theta \equiv \frac{1}{\sin \theta} \equiv \sec \left(\frac{\pi}{2} - \theta \right) \equiv \frac{\cot \theta}{\cos \theta} \,$

Funciones circulares

Las seis funciones circulares también llamadas funciones trigonométricas son: seno, coseno, tangente, cotangente, secante y cosecante. Denotadas respectivamente por: sen x, cos x, tan x, cot x, sec x, y csc x.

Definición: Si x es un número real y (a, b) son coordenadas del punto circular P(x), entonces las seis funciones circulares o trigonométricas se definen como:

P(X) = (a,b)

Con esta definición podemos evaluar las seis funciones trigonométricas de los puntos:

Ejemplos para discusión: Evaluar las seis funciones trigonométricas para:

1) P(0) : P(0) = (1, 0), donde a = 1 y b = 0

FORMAS SENOIDALES

Funciones periódicas

Una función f(x) es periódica, de período T, si para todo número entero z, se verifica:

f(x) = f(x + zT)

La función f(x) = sen x es periódica de periodo 2π, ya que cumple que:

sen (x + 2π) = sen x

La función f(x) = tg x es periódica de periodo π, ya que cumple que:

tg (x + π) = tg x

La función mantisa, f(x) = x - E(x), es periódica de periodo 1.

Frecuencia:

La frecuencia es el número de veces que una masa vibratoria o señal eléctrica repite un ciclo, de positivo a negativo (amplitud).

El desplazamiento completo de una onda, que corresponde a un giro de 360º en una circunferencia, se conoce como ciclo.

La frecuencia se mide en herzios (Hz), siendo su valor el número de veces que se repiten en un segundo.

1 Hz = 1 ciclo / 1 segundo

Amplitud de onda:

La distancia por encina o por debajo de la línea central de una forma de onda representa la amplitud de la señal. Cuanto mayor es la distancia, mayor será la variación de presión o la señal eléctrica.

La amplitud puede medirse usando varios estándares. Los máximos positivos y negativos de uina onda se conocen como valor de pico, y la distancia entre el pico negativo y positivo se conoce como valor pico a pico.

El valor medio eficaz (root meant square o RMS) se usa como vaor medio más significativo entre amos, y es el que se aproxima más al nivel percibido por nuestros oidos.

En una onda sinusoidal, el valor RMS se calvula elevando al cuadrado la amplitud de la onda en cada punto y es 0.707 veces el valor de pico. Al ser el cuadrado de un número el valor RMS siempre será un valor positivo.

Período T: Es el tiempo que transcurre hasta que la función comienza a repetirse.

Sea

un número real positivo. La función que a cada número real x le hace corresponder la potencia

se llama función exponencial de base a y exponente x.

Como

para todo

,la función exponencial es una función de

En el siguiente teorema, se presentan las propiedades más importantes de la función exponencial.

2.1.1 Teorema (Leyes de los Exponentes)

Sean a y b reales positivos y x,yÎÂ ,entonces:

6 .

Cuando a > 1 ,si x < y, entonces,

.Es decir, cuando la base a es mayor que 1,la función exponencial
de base a es estrictamente creciente en su dominio.

Cuando 0 < a < 1, si x < y , entonces,

Esto significa que la función exponencial de base a < 1 es estrictamente decreciente en

su dominio.

10.Si 0< a < b ,se tiene:

Esta propiedad permite comparar funciones exponenciales de diferentes bases.

11. Cualquiera que sea el número real positivo

,existe un único número real

tal que

. Esta propiedad indica que la función exponencial es sobreyectiva.

Cuando x e y son enteros, los propiedades enunciadas anteriormente pueden demostrarse usando las definiciones y el teorema 1. Para el caso en el cual x e y son racionales, la demostración utiliza la definición y el teorema 2. Para el caso general, es decir, cuando x e yson reales, la demostración utiliza elementos del análisis real.

Gráfica de la Función Exponencial

En relación con las propiedades 7 y 8, enunciadas en el teorema, es conveniente hacer algunos comentarios adicionales.

En primer lugar, en las figuras 1 y 2, aparecen las gráficas de algunas funciones exponenciales de base a > 1 (fig. 1) y de base a < 1 (fig. 2).

Note que cuando la base a es mayor que 1,la función exponencial

(fig.1) no está acotada superiormente. Es decir ,

crece sin límite al aumentar la variable x. Además, ésta función tiene al cero como extremo inferior. Esto es ,

tiende a cero(0), cuando x toma valores grandes pero negativos.

Igualmente, cuando la base a < 1, la función exponencial

(fig.2) no está acotada superiormente, pero su comportamiento para valores grandes de x, en valor absoluto, es diferente. Así,

crece sin límite, al tomar x valores grandes, pero negativos y

tiende a cero, cuando la variable x toma valores grandes positivos.

El hecho de ser la función exponencial

con a > 1, estrictamente creciente (estrictamente decreciente cuando 0 < a < 1), significa que la función exponencial es inyectiva en su dominio.Este hecho y la continuidad de la función son las condiciones que se exigen para garantizar la existencia de la función inversa ( función logarítmica), que se presentan en la próxima sección.

En relación con la propiedad 9, en un sentido, se deduce fácilmente de la definición de función; y, en otro, del hecho de ser la función exponencial inyectiva.

Observación.

Cuando a = e ,donde e es el número irracional cuya representación decimal con sus primeras cifras decimales, es e = 2.7182818284….,la función exponencial

,se llama: función exponencial de base e y, frecuentemente, se denota por Exp( x ) = .

Las Funciones Hiperbólicas
En algunos problemas de Física e Ingeniería, se presentan ciertas combinaciones de las funciones

que por su interés y características especiales merecen ser consideradas con algún tratamiento. Tales combinaciones reciben el nombre de funciones hiperbólicas.

Aquí solamente, se definirán y presentarán algunas identidades básicas que las relacionan.

La función COSENO HIPERBÓLICO, denotada por coshx, se define:

na función se llama logarítmica cuando es de la forma y = log a x donde la base a es un número real y positivo pero distinto de 1, puesto que el resultado sería 0.

Entonces se dan dos casos:

Base mayor que la unidad (a > 1)

Comparación: Las 3 funciones (log 2 x, log 5 x, log 7 x) se unen en el punto (1,0) porque el log a 1 = 0, y el log a a = 1, con lo que coincide que la gráfica pasa por (1,0) y (a,1).

En la función logarítmica (cuando a > 1) cuanto mayor es la base del logaritmo, más cerca del eje X está.

Las funciones de la forma y = log a x cuando la base es mayor que la unidad (a > 1) tienen las siguientes características:

(tomando como ejemplo la función f (x) = log 5 x)

-Dominio: el dominio de la función son los reales positivos puesto que no existe el logaritmo de un número negativo. Dom (f) = R +

En este tramo la función es negativa porque al introducir la antiimagen de un número racional la imagen que da, es un número negativo, lo que no quiere decir que existan imágenes para números negativos en esta función, ya que es imposible. log -x "

-Recorrido: el recorrido de la función es toda la recta real

ya que se ve como la función llega de -" y continua hacia + ".

-Continuas y crecientes: la función es creciente en todo su dominio porque...

...x < x' ! f(x) " f(x'), y continua porque todos sus puntos tienen imagen, tienen límite, y el límite de un punto coincide con la imagen del punto.

-Simetría: la función no es ni simétrica impar (por no ser simétrica respecto del origen) ni tampoco par (por no ser simétrica respecto del eje de coordenadas

no es simétrica respecto del origen

no es simétrica respecto del eje de ordenadas

-Asintotas: Partiendo del Dominio de la función ( Dom(f) = R+ ),

no se ven números concretos candidatos a asíntota por lo que viendo la gráfica deducimos que

x = 0, es una asíntota vertical y al probarlo comprobamos que es cierto.

lim log 5 x = - "

x ! 0 +

lim log 5 x = + "

x ! 0 -

No tiene asíntotas horizontales porque el limite cuando la función tiende a infinito no es un número concreto, (a simple vista se aprecia) al igual que no tiene asíntotas oblicuas.