Teniendo en cuenta la expresión general de una función cuadrática y además que f(x)=0 ,
igualamos la expresión a cero y se transforma en una ecuación cuadrática.
Para hallar los ceros de una función f(x), hay que buscar las abscisas de los puntos cuya ordenada es 0.
Para ello, planteamos f(x)=0 y despejamos, de ser posible, los valores de x que verifican la ecuación.
Ejemplos:
Busquemos las raíces de h(x)= x2 - 1 ( a=1, b=0, c= -1)
Planteamos x2 - 1=0
Despejamos x = x2 = |x|= Ö 1 =>
|x|= 1 =>x1=1 o x2= -1
Los valores x1=1 o x2= -1 son los puntos en los que el gráfico de esta función interseca al eje x.
Busquemos las raíces de g(x)= x2 + 2 ( a=1, b=0, c= 2 )
Planteamos ------------->x2 + 2 =0
Despejamos x ---------->x2 = -2
Como el cuadrado de un número real no puede ser negativo, g(x) no tiene raíces reales, es decir, no tiene puntos de contacto con el eje x.
Busquemos las raíces de g(x)= (x -3 )2
Planteamos -------------> ( x - 3 )2 =0
Despejamos x ----------> x - 3 = Ö 0
x - 3 = 0 => x = 3
El valor x=3 es el único punto en el que el gráfico de esta función interseca al eje x, dicho punto coincide con su vértice, en este caso la raíz se llama doble.
Busquemos las raíces de g (x)= x 2 + 4x ( a=1, b=4, c= 0)
Planteamos ---------------> x 2 + 4x = 0
Extraemos factor común x--> x (x + 4 ) = 0
Si x (x + 4 ) = 0 => x=0 o x + 4 =0
Despejamos x ----------> x + 4 = 0 => x = -4
Los valores x1= 0 o x2= -4 son los puntos en los que el gráfico de esta función interseca al eje x.
Busquemos las raíces de g (x)= x 2 + 2x - 3 ( a=1, b=2, c= -3)
Planteamos -------------> x 2 + 2x - 3 =0
f(x) = x2 + x - 12
Cuando lo igualamos a cero y lo resolvemos tenemos:
x2 + x - 12 = 0 Igualando a cero.
(x + 4)(x - 3) = 0 Factorizando.
x = - 4 Solución 1
x = 3 Solución 2
Puesto que x1 = - 4 y x2 = 3 son soluciones de f(x) entonces f( -4 )= 0 y f( 3 )= 0. Decimos entonces que x = - 4 y x = 3 son raíces del polinomio f(x)= x2 + x - 12
Las raíces de f(x) = x3 - 4 x2 + x + 6 son x = - 1, x = 2 y x = 3
Teoremas del factor y del residuo
Si  es el residuo de dividir el polinomio
es el residuo de dividir el polinomio  entre
entre  , entonces
, entonces  .
.
Demostración.
Como  por el algoritmo de la división, se tiene que si
por el algoritmo de la división, se tiene que si  ,
,  .
.
O sea,  .
.
Ejemplo.
Hállese el residuo de dividir el polinomio  entre
entre  .
.
Solución.
O sea que el residuo es 2.
Teorema del factor
Si  es un cero del polinomio
es un cero del polinomio  , entonces
, entonces  es un factor de
es un factor de  .
.
Demostración.
Si  es un cero de
es un cero de  ,
,  .
.
Pero por el algoritmo de la división  .
.
Como  ,
,  .
.
Por tanto,  y
y  .
.
Ejemplo
Use el teorema del factor para probar que  es un factor de
es un factor de  .
.
Solución.
Luego –1 es un cero de  .
.
Así  es un factor de
es un factor de  .
.
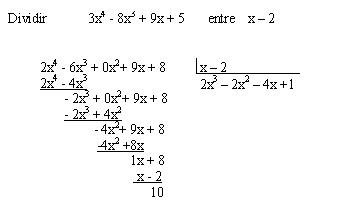
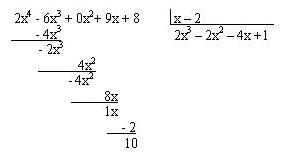
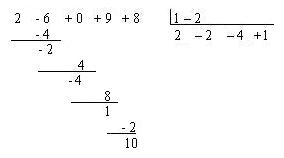
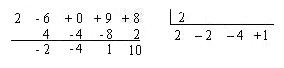
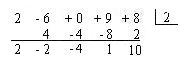

 El Teorema Fundamental del Algebra (TFA) dice que todo polinomio a coeficientes complejos tiene un raíz compleja, es decir existe un número complejo donde el polinomio evalua a cero. Hay muchas demostraciones de este importante resultado. Todas requieren bastantes conocimientos matemáticos para formalizarlas.
El Teorema Fundamental del Algebra (TFA) dice que todo polinomio a coeficientes complejos tiene un raíz compleja, es decir existe un número complejo donde el polinomio evalua a cero. Hay muchas demostraciones de este importante resultado. Todas requieren bastantes conocimientos matemáticos para formalizarlas.
División sintética
La división sintética es un procedimiento "abreviado" para determinar el cociente y el residuo que se obtiene al dividir un polinomio  de grado
de grado  , por un polinomio de la forma
, por un polinomio de la forma  , con
, con  , a partir de los coeficiente de
, a partir de los coeficiente de  y el cero de
y el cero de  .
.
El procedimiento que usaremos para realizar la división sintética de un polinomio , por un polinomio de la forma
, por un polinomio de la forma  , lo ilustraremos a través de ejemplos.
, lo ilustraremos a través de ejemplos.
El procedimiento que usaremos para realizar la división sintética de un polinomio
Comenzamos dividiéndolo normalmente
Pero resulta mucho escribir pues repetimos muchos términos durante el procedimiento, los términos restados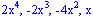 pueden quitarse sin crear ninguna confusión, al igual que no es necesario bajar los términos
pueden quitarse sin crear ninguna confusión, al igual que no es necesario bajar los términos 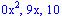 . al eliminar estos términos repetidos el ejercicio nos queda:
. al eliminar estos términos repetidos el ejercicio nos queda:
Ahora si mantenemos las potencias iguales de x en las columnas de cada potencia y colocando 0 en las faltantes se puede eliminar el escribir las potencias de x, así:
Como para este tipo de división solo se realiza con para divisores de la forma x – c entonces los coeficientes de la parte derecha siempre son 1 – c, por lo que podemos descartar el coeficiente 1 y el signo negativo, también se puede lograr una forma más compacta al mover los números hacia arriba, nos queda de la siguiente forma:
Si ahora insertamos a la primera posición del último renglón al primer coeficiente del residuo (2), tenemos que los primeros números de este renglón son los mismos coeficientes del cociente y el último número es el residuo, como evitamos escribir dos veces eliminamos el cociente.

Teorema fundamental del álgebra
 El Teorema Fundamental del Algebra (TFA) dice que todo polinomio a coeficientes complejos tiene un raíz compleja, es decir existe un número complejo donde el polinomio evalua a cero. Hay muchas demostraciones de este importante resultado. Todas requieren bastantes conocimientos matemáticos para formalizarlas.
El Teorema Fundamental del Algebra (TFA) dice que todo polinomio a coeficientes complejos tiene un raíz compleja, es decir existe un número complejo donde el polinomio evalua a cero. Hay muchas demostraciones de este importante resultado. Todas requieren bastantes conocimientos matemáticos para formalizarlas.
Sin embargo, si se deja de lado algo del rigor matemático, hay argumentos simples y creibles, que le permiten a uno convencerse de la veracidad del TFA. Nuestro objetivo es presentar a continuación uno de estos argumentos.
Consideremos entonces un polinomio P(z) cualquiera de grado n.
Luego, su n-ésimo coeficiente Pn no puede ser igual a 0. SiP(0)=0, estarímos listos pues tendríamos que 0 es una raíz de P. Supondremos entonces que se tiene el caso no trivial, es decir, queP(0) no es 0. Notar que esto significa que P0 es distinto de 0, puesto que P(0)=P0.
Si f(x) es un polinomio de grado n, con n > 0, entonces f(x) tiene precisamente n
factores lineales, es decir:
f(x) = a(x – c1)(x – c2)....(x – cn),
en donde c1, c2, .....cn son números complejos y a es el coeficiente principal de f(x).



Teorema de factorización lineal
Si f(x) es un polinomio de grado n, con n > 0, entonces f(x) tiene precisamente n
factores lineales, es decir:
f(x) = a(x – c1)(x – c2)....(x – cn),
en donde c1, c2, .....cn son números complejos y a es el coeficiente principal de f(x).




Mmm muy bueno gracias
ResponderEliminarMmm muy bueno gracias
ResponderEliminar