Donde P y Q son polinomios y x una
variable, siendo Q distinto del polinomio nulo. Las funciones
racionales están definidas o tienen su dominio de definición en
todos los valores de x que no anulen el denominador.1
La palabra "racional"
hace referencia a que la función racional es una razón o
cociente (de dos polinomios); los coeficientes de los polinomios pueden
ser números racionales o
no.
Las funciones
racionales tienen diversas aplicaciones en el campo del análisis numérico para interpolar o
aproximar los resultados de otras funciones más complejas, ya que son
computacionalmente simples de calcular como los polinomios, pero permiten
expresar una mayor variedad de comportamientos.
dominio de definición de
una función racional
Para el cálculo del dominio de las funciones con la x en el denominador o racionales, hay que tener en cuenta que el denominador de una fracción nunca puede ser nulo.
Luego los valores de x que hagan cero el denominador de la función no pueden pertenecer al dominio de la misma
Para el cálculo del dominio de las funciones con la x en el denominador o racionales, hay que tener en cuenta que el denominador de una fracción nunca puede ser nulo.
Luego los valores de x que hagan cero el denominador de la función no pueden pertenecer al dominio de la misma




Asíntotas horizontales:
Las asíntotas horizontales se refieren a la tendencia de una función. Las tendencias se descubren calculando los límites de la función para valores muy grandes (infinitos) o para valores muy negativos (menos infinito).Las asíntotas horizontales pueden ser bilaterales en un mismo valor, bilaterales con diferente valor, o unilaterales.
Hay funciones en las cuales las asíntotas horizontales no se tocan ni cruzan, hay otras en las cuales sí se puede cruzar la asíntota horizontal. En este espacio, veremos los dos casos. No hay que confundir, que las asíntotas verticales no se pueden tocar ni cruzar, ya que ellas dependen de las no definiciones de la función, y si la función no está definida en una asíntota vertical, no puede adoptar el valor de x de la asíntota vertical.
La forma de cálculo de las asíntotas horizontales ya se estudió en el capítulo de límites, en los límites hacia infinito.
Aquí se van a analizar funciones que presentan asíntotas horizontales:
1.- Desde el punto de vista funciones racionales sólo hay dos tipos que presentan asíntotas horizontales; las que tienen el grado del numerador igual o menor que el grado del denominador.
2.- También presentan asíntotas horizontales algunas funciones exponenciales así como algunas logarítmicas.
 La gráfica de la función tiene una asíntota horizontal en y = 0.
La gráfica de la función tiene una asíntota horizontal en y = 0. Si analiza uno un poco el límite calculado, se da uno cuenta que existe una diferencia entre el límite hacia oo y el de -oo.
Si analiza uno un poco el límite calculado, se da uno cuenta que existe una diferencia entre el límite hacia oo y el de -oo. Si se calcula el límite cuando x tiende hacia oo, se divide entre un número muy grande positivo, lo cual nos lleva a la conclusión, que se acerca uno a cero, por los valores positivos.
Si se calcula el límite cuando x tiende hacia oo, se divide entre un número muy grande positivo, lo cual nos lleva a la conclusión, que se acerca uno a cero, por los valores positivos.Si se calcula el límite cuando x tiende hacia -oo, se divide entre un número negativo muy grande, y la división tiende a cero, pero por valores negativos.
jo.

Estas dos observaciones son de gran importancia, ya que nos pueden dar información de por dónde se acerca la curva a la asíntota horizontal.
En el caso "x tiende a oo", se acerca por arriba.
En el caso "x tiende a -oo", se acerca por abajo.
OJO: Analícese la siguiente función, que cruza la asíntota horizontal, para poder acercarse a la asíntota por arriba viniendo de aba
 La función tiende a 0 cuando x tiende a valores muy grandes o muy negativos.
La función tiende a 0 cuando x tiende a valores muy grandes o muy negativos.Cabe mencionar, que cuando x tiende a valores muy grandes la función tiende a cero pero manifestando valores positivos. Esto implica, que se acerca a la asíntota horizontal por arriba.
 Por otro lado, si x tiende a valores muy negativos, la función tiende a cero, pero por valores negativos, lo cual nos indicaría, que se acerca a la asíntota horizontal por abajo.
Por otro lado, si x tiende a valores muy negativos, la función tiende a cero, pero por valores negativos, lo cual nos indicaría, que se acerca a la asíntota horizontal por abajo. Tiene una ASINTOTA HORIZONTAL en y = 0
Tiene una ASINTOTA HORIZONTAL en y = 0 En la gráfica se alcanza a distinguir, que del lado derecho, la función va por encima del eje "x", en cambio del lado izquierdo, se acerca por abajo.
En la gráfica se alcanza a distinguir, que del lado derecho, la función va por encima del eje "x", en cambio del lado izquierdo, se acerca por abajo.OJO: Esto tiene implicaciones serias para la función. Después de cruzar la asíntota horizontal, debe tener un máximo y un punto de inflexión, ya que de otra manera no podría acercarse a la asíntota horizontal en y = 0

La función tiene una asíntota horizontal en
y = 0
 Los dos límites tienden a cero, si hacemos el estudio, como en el primer problema, vemos que los dos límites se acercan a cero por arriba.
Los dos límites tienden a cero, si hacemos el estudio, como en el primer problema, vemos que los dos límites se acercan a cero por arriba. 

Asíntotas verticales:
Una asíntota vertical es una recta vertical, a la cual se acerca la función sin tocarla nunca.
No debe confundirse la condición de que una asíntota vertical no se toca o cruza, con el hecho, de que las funciones sí pueden cruzar o tocar una asíntota horizontal.
Para que una función tenga una o varias asíntotas verticales, se tienen que cumplir las siguientes condiciones:
1.- En x = a, la función no está definida, o sea, x = a no es parte del dominio de la función. Por esto no la puede tocar.
2.- El límite cuando x tiende a "a" de la función no existe, pero tiene que haber una tendencia de la función hacia valores extremadamente grandes (infinito) ó extremadamente negativos (menos infinito). Puede darse el caso, de que acercándose por ambos lados al valor de x = a, la tendencia del valor de la función sean ambos infinitos ó ambos menos infinito.
NOTA: Una asíntota vertical puede provocar en la función un cambio de concavidad en la función de antes de la asíntota a después de la asíntota. Analícense algunas de las gráficas de las funciones a continuación. En las primeras dos gráficas hay un cambio de concavidad antes y después de la asíntota vertical.
| | 2.- El límite en x = 3 no existe. Cuando x se acerca a 3 por la derecha el límite es: infinito Cuando x se acerca a 3 por la izquierda el límite es: menos infinito. | Por lo tanto la función tiene una Asíntota Vertical en x = 3, o sea, la recta x = 3 es la asíntota a la cual la función se va a acercar indefinidamente sin tocarla nunca. |
| | |  |
| | 1.- La función no está definida en dos valores de x, en x = 2 y en x = 4. 2a.- En x = 4 el límite no existe, por la derecha el valor de la función tiende a infinito y por la izquierda el valor de la función tiende a menos infinito. 2b.- en x = 2, el límite sí existe y es -5/2 | Por lo tanto, una de las restricciones de dominio es una Asíntota vertical, mientras que la otra, como ya se vio anteriormente es un agujero en la función. La función tiene una A. v. en x=4, o sea, la recta x = 4 funge como recta a la cual se acerca la función sin tocarla nunca. |
| | A diferencia de los límites anteriores, que no existen, los límites cuando x tiende a 2, sí existen. por lo tanto, el límite cuando x tiende a 2, sí existe: |  |
| | Es conveniente hacer notar, que este es un caso en que la función cruza la asíntota horizontal, lo cual se verá con más detenimiento en la sección de asíntotas horizontales. |  |
| | La función no está definida para valores iguales o menores que 4. | La gráfica de la función será únicamente de (-4,oo). Mostrará una asíntota vertical en x = 4, ya que la función tiende a menos infinito. |
| Este límite es menos infinito, nos da la tendencia de la función, de decrecer conforme x tienda a 4 por la derecha. | Este límite no se puede calcular, ya que me quiero acercar al 4 por la izquierda y los valores menores a 4 no están en el dominio de la función. |  |
| | El dominio está restringido a valores de x menores que -1 y mayores que 1. | Tiene dos asíntotas verticales, una en x = -1 y otra en x = 1. Se nota, que estas asíntotas son unilaterales, ya que la función no tiene definición entre x = -1 y x = 1 |
El límites cuando x tiende a -1 por la derecha no se puede calcular, así como el límite cuando x tiende a 1 por la izquierda. | En esta función, como en la anterior hay dos límites que no se pueden calcular, ya que se acerca uno al valor de x con valores que están fuera del dominio. |  |
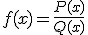
No hay comentarios:
Publicar un comentario